Généralités

v Introduction :

Physique & biologie ?

® Filière scientifique, non ?

Prétention de la physique : compréhension d’objets inertes, des plus petits aux plus grands.

Physique ancienne :

Le voyage sur la Lune était déjà, théoriquement, possible

(Il manquait juste des petits détails pratiques…)

+ Concept de continuité de la matière (lumière, matériaux comme une planche de bois)

Or, c’est faux !

La lumière est discontinue (émission de particules), une planche de bois n’est qu’un assemblage de vide.

® Physique moderne : Changement de vision des choses

Tout est discontinu

Maintenant, il est possible de calculer une probabilité de position d’un électron autours d’un atome.

v Les objets de l’univers :

Ø L’univers :

Âge : 13,7.10⁹ ans

Soit 4,32.10¹⁷ secondes

Son origine est le BIG-BANG, une explosion de matière dont de la lumière. De là, on peut deviner sa taille :

v = d / t d = c . t = 3.10⁸ m.s^–1 . 4,32.10¹⁷ s.

Taille : 1,3.10²⁶ m.

Une telle distance est inconcevable en mètres, il faut chercher une autre unité : les années–lumière (= la distance que la lumière parcourt en 1 année)

1 année-lumière = 365 . 24 . 3 600 . 3.10⁸

= 9,48.10¹⁵ m

Taille : 13,7.10⁹ années-lumière.

Ø Le domaine humain :

= dimensions à l’échelle humaine :

Plus grand : quelques dizaines ou centaines de kilogrammes, mètres, secondes, heures ou jours. Plus petit : quelques micromètres.

Ø L’atome :

Ordre de grandeur : l’angström 1 Å = 10^–10 m.

Il est constitué d’un noyau et d’électrons. Le noyau est constitué de A nucléons.

dont Z protons,

+ A – Z neutrons.

L’ensemble des protons – neutrons constitue les nucléons (composés chacun de 3 quarks)

Tout atome est neutre : les électrons sont au même nombre que les protons : Z.

Un élément chimique est défini par le nombre Z de protons dans le noyau.

La masse de la matière est exclusivement dans le noyau. m = 1,66.10^–27 kg. La masse d’un électron est 1836 fois moindre.

Noyau 100 m de vide Électron

( 1mm) ( 1 µm)

Dimensions . 10¹²

Ø Notion de temps :

Univers	Temps de vie :	13,7.10⁹ ans = 4,7.10¹⁷ s
Homme	Temps de vie :	75 ans = 2.10⁹ s
Atome	Période de vibration :	10^–14 s
Noyau	Temps de la lumière pour le traverser :	3.10^–24 s

v Interactions entre ces objets :

Ø Interaction gravitationnelle :

= force de gravité.

Découverte par Newton.

= Force entre 2 objets massiques.

m₁ . m₂

F_G = G . G = 6,67.10^–11 MKSA

d²

C’est elle qui gouverne le cosmos, le mouvement des planètes, les marées, la gravité.

Ø Interaction électromagnétique :

= Force entre 2 objets chargés.

1 q₁ . q₂ 1

F_E = . = 9.10⁹ MKSA

4. π . e₀ d² 4. π . e₀

C’est cette force qui gère l’interaction entre 2 objets chargés, mais aussi les frottements (résistance) La charge électrique en mouvement entraîne une force magnétique sur une autre charge électrique.

Le noyau pose problème : les protons (particules chargées à l’intérieur du noyau) se repoussent.

Ø Interaction nucléaire forte :

Elle assure la cohésion du noyau et la cohésion des quarks dans le nucléon. Leur découverte reste empirique : on ne visualise que leurs effets. On sait que leur portée est petite, de l’ordre du noyau (10^–15 m) et suffisamment forte pour contrecarrer la force électromagnétique.

Ø Interaction nucléaire faible :

Elle permet de modifier les quarks de type U en type D et vice–versa. Cela entraîne la transformation de proton en neutron et réciproquement.

Elle est 10⁶ moins forte que l’interaction nucléaire forte et sa portée est de 10^–18 m. Mais elle explique le phénomène de fusion des atomes d’Hydrogène en atome d’Hélium dans le soleil. Sans cette fusion il n’y a pas d’énergie nucléaire, donc pas de soleil et donc aucune vie possible sur la Terre.

Proton (charge +) " Neutron + b⁺ + 1 neutrino

_{A A 0}

X " Y + b⁺ + 1 neutrino

Z Z–1 1

Þ Radioactivité b ⁺ b⁺ : électron qui porte une charge + e (= anti–électron)

Neutrino : particule sans masse (ou très faible)

qui a une interaction quasi nulle

avec la matière.

Neutron " Proton + bˉ + 1 antineutrino

_{A A}

X " Y + bˉ + 1 antineutrino

Z Z+1

Þ Radioactivité bˉ bˉ : électron « classique » qui porte une charge – e.

On utilise le « b » pour indiquer que cet électron n’est pas originaire du cortège électronique.

bˉ et b⁺ = particule et antiparticule.

La rencontre d’une particule avec son antiparticule entraîne une disparition de la matière et une libération d’énergie sous forme de photons.

Ce processus est utilisé dans l’imagerie médicale avec l’émission de b⁺ qui, une fois qu’ils rencontrent de la matière, rencontrent forcément des électrons.

Rayonnement g

( b⁺ ; eˉ ) et disparition de la matière.

Comprendre un atome avec la précision la plus fine :

" Comprendre un noyau :

9 Calcul des 4 interactions entre les nucléons 2 à 2.

Possible quand il n’y en a pas trop, comme l’Hydrogène ou Hélium…

Après cela devient vite impossible, même pour un ordinateur…

+ Calcul des 4 interactions avec et dans le cortège électronique.

C’est déjà fini avant d’avoir commencé…

Alors essayer de comprendre 2 atomes...

À l’échelle macroscopique :

On ne considère pas les manifestations des interactions entre les atomes ; il suffit de travailler avec les forces gravitationnelles et coulombienne.

À l’échelle de l’atome :

On ne cherche pas à voir ce qui se passe à l’intérieur du noyau ; il suffit de travailler avec la force coulombienne (la force gravitationnelle est négligeable)

À l’échelle du noyau :

On ne travaille qu’avec les interactions Proton – Proton : la force coulombienne et l’interaction nucléaire forte.

Même avec 2 forces seulement, c’est déjà compliqué…

v Mesures d’une grandeur – Outils et méthodes :

Expérience " mesures " corrélation entre les des différentes mesures.

Les quantités fondamentales : Longueur – Temps – Masse – Intensité électrique

Les unités du Système International SI ou MKSA :

Longueur : le Mètre, m

Masse : le Kilogramme, kg

Temps : la Seconde, s

Intensité de courant : l’Ampère, A

+ Température : le Kelvin, K

Quantité de matière : la Mole, mol

Ø La longueur :

10^–6 m	1 µm (cellule)
10^–9 m	1 nm (molécule)
10^–10 m	1 Å (atome)
10^–12 m	1 pm = 1 picomètre
10^–15 m	1 fm (noyau)

Défini par un mètre étalon en alliage de titane. Mais une définition vis–à–vis d’un objet est risquée car l’objet peut être perdu.

" 1 mètre = distance parcourue par la lumière en un temps de 1/299792458 seconde.

10^–3 kg	1 g
10^–6 kg	1 mg
10^–9 kg	1 µg
10^–12 kg	1 ng
10^–18 kg	1 fg

Ø La masse :

Défini par un kilogramme étalon, il en existe 10 exemplaires précieusement gardés.

= propriété de tout objet qui, lorsqu’il est en présence d’un autre objet, l’attire.

1 atome : 1,66 . 10^–27 kg

" 1u.m.a = 1 unité de masse atomique

= 1/12 de la masse d’un atome de carbone ¹²C.

La masse d’une mole (soit N_A atomes) de ¹²C = 12 g

1 . 12 . 10^–3

Donc 1 u.m.a = = 1,66 . 10^–27 kg

12 . 6,03 . 10²³

Ø Le temps :

Au départ, on observait une périodicité (jour–nuit ; saisons)

Maintenant, on définit la seconde à partir des vibrations de l’atome de Césium 133.

" 1 seconde = le temps que l’atome de Césium vibre 9 192 631 770 fois.

On obtient un temps différent selon que l’on est au niveau de la mer ou en altitude : ceci est dû à la gravitation.

Ø L’énergie :

La masse peut disparaître : ce n’est pas une unité fiable. L’énergie est partout et est fiable. C’est une quantité fondamentale dans le sens où, sans énergie, on ne fait rien.

Exemple : les réserves de pétrole :

À activité constante (sans tenir compte de l’émergence de la Chine et de l’Inde), elles seront vides dans 50 à 70 ans.

Unité :

- En MKSA : le Joule

- En cm g s : l’erg

- Pour l’atome : l’eV

1 eV = l’énergie donnée à un électron quand on le soumet à un potentiel de 1 Volt.

10³ eV	1 keV
10⁶ eV	1 MeV

E = q . V

= 1,6 . 10^–19 Coulomb . 1 Volt

= 1,6 . 10^–19 Joule

Ø Dimension et analyse dimensionnelle :

Soit : [ L ] ; [ M ] et [ T ]

Distance = d Û [ L ] Vitesse = v = d/t Û [ L ] . [ T ]^–1

Accélération = a = v/t Û [ L ] . [ T ]^–2 Force = m.a Û [ M ] . [ L ] . [ T ]^–2

Énergie = ? On recherche des expressions de l’énergie :

E = m.c² = [ M ] . [ L ]² . [ T ]^–2

E = m.g.h = m.a.h = [ M ] . [ L ]² . [ T ]^–2 ( g = a)

Avec 2 expressions, on obtient une même dimension : ça ne veut pas dire que l’on a forcément bon, mais ça veut au moins dire que cette relation n’est pas délirante.

1 Joule = 1 kg . (1 m)² . (1 s)^–2

= 10³ g . 100² cm² . s^–2

= 10⁷ g.cm².s^–2

= 10⁷ erg.

Soit 2 grandeurs A et B :

Si A = B Þ [ A ] = [ B ]

Mais Si [ A ] = [ B ] ¹> A = B

E = h . n = h . c /l h = 6,626 . 10^–34 J.s

E = k /l

(eV) (Å)

" Trouvons k :

Soit la gamme du visible : 4000 à 8000 Å

(m.s^–1)

E = h . c /l

(J) (J.s) (m)

(eV) 6,626 . 10^–34 . 3 . 10⁸ . 10¹⁰ (Å.s^–1) 12 400 (eV. Å) = k

E = =

1,6 . 10^–19 . l (Å) l (Å)

Si l = 4 000 Å alors E = 3,1 eV

l = 8 000 Å alors E = 1,55 eV

T = période = f( m, g, l )

ℓ

T = m ^A . g ^B . ℓ ^C

m, g [ g ] = [ L ] . [ T ]^–2

[ T ]¹ = [ m ] ^A . [ g ] ^B . [ ℓ ] ^C

[ T ]¹ = [ M ] ^A . [ L ] ^B . [ T ] ^–2B . [ L ] ^C

[ T ]¹ = [ L ] ⁰ . [ T ] ¹ . [ M ] ⁰

Donc : –2B = 1 Þ B = – ½

A = 0

B + C = 0 Þ C = ½

D’où : T = √(ℓ /g) . 2π

Ø Chiffres significatifs :

On peut : Compter " valeur exacte

Mesurer " incertitude

Soit une longueur mesurée ℓ = 41,55 cm

On émet des doutes sur le dernier chiffre, on ne garde que 3 chiffres significatifs.

Autre exemple :

E = a . C avec C = 2 250

On mesure : E = 30,85 keV Þ a = 0,013 711 111 11

Si on reprend le calcul de E avec des valeurs plus ou moins précises de a déterminée à partir de la mesure :

a = 0,013 711 111 11	E = 30,85
a = 0,013 711	E = 30,84975
a = 0,013 71	E = 30,8475
a = 0,013 7	E = 30,825
a = 0,014	E = 31,5
a = 0,01	E = 22,5

Ø Les incertitudes sur les mesures :

Soit La mesure d’une grandeur X donnant un résultat x,

Et le résultat réel : x₀.

L’erreur : e = x – x₀ Soit positive, soit négative.

L’incertitude : Dx = |e| On prend toujours l’arrondi au dessous.

L’incertitude relative : Dx / x₀ Problème : on ne connaît pas x₀ !

" Dx / x

Exemple :

La masse du soleil = 1,9889 ± 0,0030 10³⁰ kg

DM /M = 0,0020 /1,9889 = 1,508 . 10^–3

La masse de la Terre = 5,974 ± 0,009 10²⁴ kg

DM /M = 0,009 /5,974 = 1,506 . 10^–3

Mesure directe :

On mesure : x " Dx = D_R + Dx _ℓ + D x_E

Réglage Lecture Étalonnage

Mesure indirecte :

On a mesuré :

B DB A avec une erreur DA

B avec une erreur DB

Périmètre = 2 (A+B) = P

" DP = (P_MAX – P_MIN)/2

2 (A + DA + B + DB) – 2 (A – DA + B – DB)

= 2 (DA + DB) P₀ = P ± DP

Surface = A . B = S

" DS = (S_MAX – S_MIN)/2

(A + DA) . (B + DB) – (A – DA) . (B – DB)

A.B + A.DB + DA.B + DA.DB – A.B + A.DB + DA.B – DA.DB

= A . DB + DA . B

S_V = S ± DS

D f d f

f’(x) = =

D x (x " 0) d x

S = f ( a , b )

d S d S

dS = . da + . db

d a d b

= b . da + a . db

dS dS

Þ DS = . Da + . Db = b . Da + a . Db

da db

Exemples de fonction :

Soit une grandeur G

et 2 quantités mesurées a et b.

Relation :	Dérivée :	Incertitude :
G = a + b	dG = da + db	DG = Da + Db
G = a – b	dG = da – db	DG = Da + Db
G = a . b	dG = a.db + b.da	DG = \|a\|.Db + \|b\|.Da
G = a / b	a.db – b.da dG = b²	\|a\|.Db + \|b\|.Da DG = b²
G = a^m	dG = m.a^m^–1 . da	DG = \|m.a^m^–1\| Da
G = e^a	dG = e^a . da	DG = e^a . Da
G = ln( a )	dG = da / a	DG = Da / a

TP émission a :

y_B

y_A

x_A x_B X

L = √ ( X² + Y² ) X = x_B – x_A et Y = y_B – y_A

Avec les incertitudes : Dx_A, Dx_B, Dy_A, Dy_B.

L² = X² + Y² que l’on dérive :

2L . dL = 2X . dX + 2Y . dY

dL = X/L . dX + Y/L . dY

|X| |Y|

DL = . DX + . DY

L L

Mesure d’une grandeur fixe : (rare)

Domaine de compatibilité

" Ça vaut le coût de faire plusieurs mesures de la même grandeur.

Mais il n’est pas possible d’effectuer plusieurs fois la mesure d’une même grandeur dans un système dynamique !

Mesure de 2 grandeurs :

Comportement linéaire :

" Soit la loi n’est pas linéaire ; soit la dernière valeur n’est pas bonne.

Comptage d’un phénomène géré par une probabilité :

Exemple : la probabilité qu’un traitement donné a un effet donné sur une espèce donnée.

On fait systématiquement une erreur statistique en ne prenant pas en compte des fluctuations.

Nombre de

lapins morts

" Distribution de Poisson

Nombre de fois

que l’on trouve

n lapins morts.

v Notion de relativité :

Soit 2 repères : R, le repère fixe et R’, le repère mobile.

Et les vitesses : v, la vitesse de quelqu’un qui marche à pied par rapport à R ;

v’, la vitesse d’un train par rapport à R ;

V, la vitesse de quelqu’un qui marche dans un train et dans le même sens de déplacement que ce dernier par rapport à R.

R R’

v’ v

V = v’ + v

0 0’

x_B – x_A Dx

v = =

t_B – t_A Dt

La vitesse de la lumière :

Pendant quelques millisecondes, on peut considérer que la Terre a un mouvement rectiligne uniforme.

La mesure de la vitesse de la lumière dans R et R’ est la même

Or, avec la mécanique classique c’est impossible : remise en cause totale !

Travaux d’Einstein :

x_A x_B x’_A x’_B

R R’

t_A t_B t’_A t’_B

x_B – x_A x’_B – x’_A

v = v’ =

t_B – t_A t’_B – t’_A

x_B – x_A ¹ x’_B – x’_A

Or : v = v’

Donc : t_B – t_A ¹ t’_B – t’_A

" Le temps n’est plus une grandeur absolue.

Cela remet en cause toutes les théories incluant le temps.

m₀

m = m : masse ; m₀ : masse au repos

√(1 – v²/c²)

10 ans après, les mathématiciens ont démontré que cette formule est la seule à pouvoir expliquer ce phénomène.

m₀ . v

Impulsion d’une particule = p = m.v =

√(1 – v²/c²)

E₀ = m₀ . c²

m₀ . c²

E_Total = E_T = m.c² = E_T = E₀ + E_C

√(1 – v²/c²) m₀ . c²

√(1 – v²/c²)

m₀ . c²

E_C = – E₀ = m₀ . c² (1 – v²/c²)^–^½ – 1

√(1 – v²/c²)

On travaille régulièrement avec des vitesses largement inférieures à la vitesse de la lumière :

(1+e)^N = 1 + Ne + N(N–1) e²/2! + …

(1 – v²/c²)^–^½ = 1 – ½ . (– v²/c²) = 1 + ½(v²/c²)

E_C = m₀ . c² . (v²/2c²) = ½ m₀ . v²

" Il s’agit de la forme classique de l’énergie cinétique.

Que se passe–t–il si l’on travaille avec les électrons ?

m₀ = 9,1 . 10^–31 kg E₀ = 9,1 . 10^–31 . (3 . 10⁸)² = 8,9 . 10^–14 J = 511 keV

Valeur de référence à connaître.

Calcul de la vitesse d’un électron :

m₀ . c² E₀

E_T = E₀ + E_C = =

√(1 – v²/c²) √(1 – v²/c²)

E₀ E₀ ²

√(1 – v²/c²) = (1 – v²/c²) =

E₀ + E_C E₀ + E_C

E₀ ² E₀ E₀

(v²/c²) = 1 – = 1 + . 1 –

E₀ + E_C E₀ + E_C E₀ + E_C

E_C 2 . E₀ + E_C

( v/c ) = .

E₀ + E_C E₀ + E_C

" Il s’agit de la forme relativiste (= absolue) utilisable pour toutes les particules.

Avec la physique classique, on obtient :

Ec = ½ . m₀ . v² = ½ . m₀ . c² . (v² /c²)

(v² /c²) = 2.E_C /m₀

( v/c ) = √(2.E_C /m₀)

Pour un électron à différentes énergies cinétiques :

E_C	( v/c) classique	( v/c) relativiste	Écart
E₀/100 = 5,11 keV	0,141	0,140	0,7 %
E₀/10 = 51,1 keV	0,447	0,416	7 %
E₀ = 511 keV	1,414	0,866	63 %

Et encore, on n’a pas pris de grandes énergies cinétiques ; dans une réaction nucléaire, un électron peut avoir quelques MeV.

Déjà, via la méthode de la physique classique, la dernière valeur est délirante :

L’électron serait 1,4 fois plus rapide que la lumière !? ...

E₀ Si : v " c,

E_T = E₀ + E_C = v/c " 1,

√(1 – v²/c²) v²/c² " 1,

1 – (v²/c²) " 0,

√(1 – v²/c²) " 0,

E₀ /√(1 – v²/c²) " ∞

Le calcul relativiste est nécessaire pour une particule ayant une vitesse supérieure à 0,1 c. Avant, l’approximation de la physique classique est admise.

E₀

E_T =

√(1 – v²/c²)

E₀² m₀ . v

E_T² = Impulsion p =

(1 – v²/c²) √(1 – v²/c²)

m₀² . v² . c² m₀² . v² . c²

p² . c² = p² . c² + m₀².c⁴ = + m₀².c⁴

(1 – v²/c²) (1 – v²/c²)

m₀² . v² . c² + m₀².c⁴ – m₀².c⁴.v²/c²

p² . c² + m₀².c⁴ =

(1 – v²/c²)

m₀².c⁴

p² . c² + m₀².c⁴ = = E_T²

(1 – v²/c²)

E_T = E₀ + E_C = √( p² . c² + m₀².c⁴ ) " Expression relativiste

Le cas d’un photon :

m₀ = 0 E₀ = m₀ . c² = 0

?? Le photon n’aurait pas d’énergie ? Si !!

E_T = E₀ + E_C = √( p² . c² + m₀².c⁴ )

= √( p² . c² ) = p . c

p = E_T/c

" Le photon transporte de l’énergie et d’impulsion.

Calcul des énergies au repos :

Particule :	Masse :	Énergie au repos : E₀ = m₀ . c²
Électron	9,1 . 10^–31 kg	511 keV
Nucléon	1 u.m.a = 1,66 . 10^–27 kg	931,5 MeV
Proton	1,00782 u.m.a	938,272 MeV
Neutron	1,00866 u.m.a	939,563 MeV

m₀ _Électron » 1/2000 . m₀ _Nucléon

Þ E₀ _Électron » 1/2000 . E₀ _Nucléon

Explication de E = m . c² :

_{A A 0}

Rayonnement b⁺ : X ® Y* + b⁺ + n

^{Z Z–1 +1}

b⁺ : positron = anti–électron

Ce b⁺ est émis avec une certaine impulsion dans la matière. Il y est freiné au point que sa vitesse devient nulle. Il va être attiré par le premier électron qui passe (attraction de 2 charges électriques opposées) Ils vont se regrouper en un point précis :

g₁

( b⁺ ; eˉ ) " émission de photons g.

Conservation de l’énergie : E = 2 . m₀. c² = Eg₁ + Eg₂

L’impulsion d’entrée = l’impulsion de sortie

p_E = p_S p_E = 0

Ils sont à l’arrêt

0 = p_S = p _g₁ + p _g₂

|p _g₁| + |p _g₂| = E _g₁ /c + E _g₂ /c

E _g₁ = – E _g₂ (angle à 180°)

E _g₁ = E _g₂ = m₀ . c² = 511 keV

Application : IM par émission g–g.

On prend un noyau (ou atome) émetteur b⁺ que l’on insert dans une molécule biologique et on l’intègre dans l’organisme.

On place le patient dans un cylindre (= ensemble de détecteurs de g) appelé caméra TEP.

Les capteurs détectent les photons g₀ à partir des g détectés à 180 ° et d’énergie 511 keV.

On arrive à converger vers l’organe où la molécule s’est intégrée.

" Visualisation de l’organe qui a fixé la molécule marquée.

Exemple d’application sur le cerveau :

La maladie de Parkinson résulte de la perte de neurones dopaminergiques. Ces neurones sont caractérisés par la fixation de Fluor.

Lorsque l’on effectue une greffe, on vérifie son évolution en injectant au patient du ¹⁸Fluor qui émet des b⁺. Si, lors de l’IRM, on observe des taches signifiant un rayonnement g, cela indique que la greffe a pris.

En demandant au patient de penser à des souvenirs datant de 10 ans, on voit évoluer les tâches nous permettant de visualiser la ou les zones qui travaillent.

v Rayonnement électromagnétique : Onde & corpuscule :

Ø Notion d’ondes et de particule :

La particule : Objet massique, localisé : x ; y ; z ; t

" de là, on peut déterminer sa vitesse v : v_X ; v_Y ; v_Z ; t

L’onde : Perturbation – Déformation – Vibration

Elle n’est pas localisable.

De ce fait, elle est difficile à définir...

On travaillera avec l’exemple le plus simple : le mouvement ondulatoire de la corde.

Ø Propriété ondulatoire : la propagation :

Prenons notre exemple : pour une corde que l’on fait onduler selon un mouvement sinusoïdal entretenu, on peut définir par une fonction : Y( x, t ) = a . sin( w.t – k.x )

x à un temps t.

(" photo)

Y(x, t) : Déformation,

w : Pulsation,

t : Date,

k. : Vecteur d’onde,

x : Position.

§ Périodicité :

Périodicité temporelle : Il existe un temps T tel que : Y( x, t+T ) = Y( x, t )

a . sin[ w.(t+T) – k.x ] = a . sin( w.t – k.x )

q’ ( q + q’ )

" sin( q + q’ ) ¹ sin( q ) + sin( q’ )

" sin( q + 2π ) = sin ( q )

Û w.t + w.T – k.x = w.t – k.x + n.2π (à n tours près ;

pour faciliter l’équation,

Û w.t + w.T – k.x = w.t – k.x + 2π on prend n = 1)

Û w.T = 2π Û T = 2π/w

Périodicité spatiale :

Il existe une longueur l telle que : Y( x+l, t ) = Y( x, t )

a . sin[ w.t – k.(x+l) ] = a . sin( w.t – k.x )

Û w.t – k.x – k.l = w.t – k.x + n.2π (à n tours près ;

pour faciliter l’équation,

Û w.t – k.x – k.l = w.t – k.x – 2π on prend n = –1)

Û k.l = 2π Û l = 2π/k

= longueur d’onde

Y( x, t ) ; Y( x, t+dt )

x – x+dx

Y( x, t ) = Y( x+dx , t+dt )

a . sin( w.t – k.x ) = a . sin[ w.(t+dt) – k.(x+dx) ]

Û w.t – k.x = w.t + w.dt – k.x – k.dx

Û w.dt = k.dx

Or, la vitesse : v = dx /dt = w/k

2π/T

2π/l

= (2π/T) . (l/2π)

v = l/T Þ l = v . T

et avec la vitesse de la lumière :

l = c . T

§ Interférence :

Écran

Exemple :

S₁ point P

Source

S₂

" Interférence destructive " Interférence constructive

(il n’y a pas de tache lumineuse au point P) (il y a une tache lumineuse au point P)

La nature des interférences dépend de la distance source – écran et du temps.

l 2l Si : S₂ – S₁ = n.l

" Interférence constructive.

Si : S₂ – S₁ = n.l + l/2

" Interférence destructive.

l/2

§ Diffraction :

Écran

lumière par

Propagation rectiligne

Lumière par

diffraction

Ø Propriété corpusculaire :

§ Démonstration par des exemples :

· Éclairage de la roue à barreaux :

Soit une roue aux frottements négligeables (roulement à bille) et bien équilibrée.

On pose sur chaque barreau :

- Une feuille de papier noir (sur un coté)

- Et une feuille d’aluminium (sur l’autre coté)

Quand on allume la lampe, la roue se met en mouvement.

Cela démontre qu’il y a transport de quantité de mouvement (impulsion et énergie)

· La cellule photoélectrique :

Intensité

Anode

Photons électrons V +

Cathode

Lorsque l’on allume la lumière, on mesure une intensité électrique.

Les photons qui frappent la cathode arrachent des électrons.

Cela démontre un état corpusculaire des photons à une certaine énergie (à une certaine longueur d’onde)

Anode

F = q . E

F est la force créée E F

par le potentiel Électron

du générateur.

Cathode

q est négatif, le champ électrique E est dans le sens opposé de la force F.

Si le potentiel de la pile n’est pas assez puissant, alors le champ n’est pas puissant. La probabilité que les électrons arrachés soient récupérés par l’anode est, elle aussi, réduite. Les électrons peuvent être réabsorbés soit dans la cathode, soit dans le gaz résiduel.

I₁

I₂ < I₁

Lorsque l’on utilise des filtres, limitant la lumière à certaines longueurs d’ondes, il n’y a plus d’électricité.

E_g = h . n Te = h . n – E_L

= énergie cinétique des électrons

U₀ = Potentiel d’arrêt E_L = Énergie de liaison des électrons

q . U₀ = h . n – E_L

Un photon correspond à un quantum d’énergie :

E = h . n = h . c / l = 12397 eV.Å / l (en Å)

Pour un champ uniforme :

F = q . E = – dE_P /dx . u_X E = – dV/dx . u_X |E| = V/d

Si E_Photon < E_L , il n’y a pas d’électrons d’arrachés " Intensité est nulle.

Exemple :

l = 7 000 Å (par un filtre) " E_g » 1,77 eV

" I = 0

Si l < 7 000 Å " I ¹ 0

Cellule à vide :

Cellule à gaz :

Quand Te > E_{Liaison
moléculaire},

il y a une ionisation.

½ m . v² = q . V

Potentiel d’ionisation

Interactions du rayonnement avec la matière

Dans la matière, on rencontre des particules massives et chargées : les électrons, les ions, les particules α, … et des particules neutres massives : les neutron et non massives : les photons.

L’existence de différentes particules induit l’existence de différentes interactions.

Les particules chargées " Interaction coulombienne avec les électrons.

Les particules neutres :

Neutrons " Interaction nucléaire (probabilité très faible)

Photons " Interaction électromagnétique avec les électrons mais non coulombienne.

v Interactions photon – matière :

Soit un matériau d’une épaisseur e

N₀ N₍_e₎ < N₀

(absorption dans la matière)

N₍_x₎ N₍_{x
+ dx}₎

dN = N₍_{x
+ dx}₎ – N₍_x₎ (dN est négatif)

Soit µ, la probabilité d’interaction d’un photon par unité de longueur de matériau traversé :

dN = – µ . dx . N(x)

On prend un dx tendant vers 0, permettant un calcul infinitésimal. On obtient alors une équation différentielle du 1^er ordre :

dN/dx + µ . N(x) = 0

dN/ N(x) = – µ . dx

" ∫ dN/ N(x) = ∫ – µ . dx

Ln (N) = – µ . x + C

N = exp(– µ . x + C)

N = exp(C) . exp(– µ . x)

Détermination de exp(C) : Avec les conditions initiales : N(0) = N₀

N(0) = exp(C) . exp(0)

N(0) = exp(C)

Þ N(e) = N₀ . exp(– µ . e)

0 x₁ x₂

S Détecteur

N₀

N(x₁) N(x₂)

N( x₁) = N₀ . exp(– µ . x₁)

N( x₂) = N₀ . exp(– µ . x₂)

Ln N

Ln N( x₁) = – µ . x₁ + Ln N₀ pente = – µ

Ln N( x₂) = – µ . x₂+ Ln N₀

Qu’est – ce que µ ?

Il s’agit du processus d’interaction des photons dans la matière.

3 Processus :

- Effet photo–électrique,

- Effet Compton,

- Matérialisation (= création de paires eˉ; e⁺)

Ø Effet photo–électrique :

Eg eˉ

T_e = Eg – E_L

Il est dominant à basse énergie : Eg inférieur à 500 keV.

Il s’agit d’un processus à seuil : Eg > E_L

Probabilité Couche L

Couche K

De plus, il y a une réorganisation du cortège électronique :

Rayons X

ou électron Auger

L K

Ø Effet Compton :

Il est dominant pour Eg » 1 MeV. On parle de diffusion :

Il est basé sur la conservation de l’énergie et d’impulsion.

g’ Eg’ ; Pg’

Eg ; Pg E₀

g eˉ j

T_e ; E₀ ; P_e

eˉ

E₀ = m_e . c² Eg = Pg . c

Équation de la relativité : E_Totale² = P_e² . c² + E₀^2.

(E₀ + T)² = E₀² + T² + 2 W₀_T " E₀² + T² + 2 E₀T = P_e² . c² + E₀²

" P_e² . c² = T² + 2 E₀T

Conservation de E_Totale : Eg + E₀ = Eg’ + E₀ + Te Eg = Eg’ + Te.

Il s’agit de la conservation d’énergie classique que l’on retrouve dans toute diffusion élastique.

Conservation de P : Pg = Pg’ + P_e

Y

Pg q

Projections sur les axes : x : Pg = Pg’ . cosq + P_e . cosj

y : 0 = Pg’ . sinq – P_e . sinj

Mais on a plusieurs inconnues : Eg’ ; T_e ; q ; j

" Eg’ est fonction de Eg et de q.

P_e² = (Pg – Pg’.cosq)² + (Pg’² . sin²q)

= Pg² + Pg’².cos²q – 2.Pg.Pg’.cosq + Pg’².sin²q

P_e² = Pg² + Pg’² – 2.Pg.Pg’.cosq

P_e² . c² = Pg². c² + Pg’². c² – 2 . Pg. c² . Pg’. c² . cosq

Eg² = Pg² . Pg’² + m₀² . c⁴

Pour un photon : Eg = Pg . c

Pour un électron : E_e² = P_e² . c² + m₀² . c⁴ = (m₀ . c² + T_e )²

= m₀².c⁴ + T_e² + 2.T_e.m₀ . c²

P_e² . c² = T_e . (T_e + 2.m₀.c²)

= Pg². c² + Pg’². c² – 2 . Pg. c² . Pg’. c² . cosq

T_e . (T_e + 2.m₀.c²) = Eg² + Eg’² – 2 . Eg². Eg’² . cosq

= (Eg – Eg’) (Eg – Eg’ + 2.m₀.c²)

= Eg² – Eg.Eg’ + 2.Eg.m₀.c² – Eg.Eg’ + Eg’² – 2.Eg’.m₀.c²

– 2.Eg.Eg’.cosq = –2.Eg.Eg’ + (Eg–Eg’).2.m₀.c²

2.Eg.Eg’.(1–cosq) = (Eg–Eg’) . 2.m₀.c²

1/( m₀.c²) . (1–cosq) = (Eg–Eg’) /(Eg.Eg’)

= (Eg) /(Eg.Eg’) – (Eg’) /(Eg.Eg’)

1/( m₀.c²) . (1–cosq) = 1/Eg’ – 1/Eg

Si q = 0 :

1/Eg’ – 1/Eg = 0 " Eg’ = Eg

Et comme : Eg = Eg’ + T_e Alors : T_e = 0

Si q = 180 :

" Il s’agit d’un cas limite.

1/Eg’ – 1/Eg = 2 /511 m₀c² = 511 keV (1–cosq) = 2

Et comme : Eg = Eg’ + T_e Alors : T_e = Eg – Eg’

Exemple :

¹³⁷Cs " E = 662 keV

Effet photo–électrique : E = E_L + T_e " E _{Transférée au milieu}

Effet Compton : E _{Transférée à l’électron} va de T=0 à T_MAX

1/Eg’ – 1/662 = 2/511 " Eg’ = 185 keV Eg = Eg’ + T_e

(" Max de l’énergie transférée par le photon)

" T_MAX = 478 keV

Maximum

Plateau Compton

Effet photo–électrique

Effet Compton

Énergie déposée

T_MAX Eg

1/Eg’ – 1/Eg = 1/( m₀.c²) . (1–cosq) = (1–cosq) /511

Cas de Eg très grand :

Eg >> 511 keV

1/Eg << 1/511 Donc : 1/Eg’ » (1–cosq)/511

Eg’ » 511 keV

" T_e = Eg – Eg’ » Eg

Par effet Compton, si l’énergie du photon est grande, ce photon transmet une grande énergie T_e @ Eg dans la matière.

Cas de Eg très petit :

Eg << 511 keV

1/Eg >> 1/511 Donc : 1/Eg’ » 1/Eg

" Eg’ » Eg

Si Eg << 511 keV, Alors, il y a diffusion :

Eg’ @ Eg

L’électron a une énergie bien supérieure à celle du photon. Il ne bouge pas (ou peu) lors du choc et le photon est diffusé.

Ø Matérialisation :

La masse peut être transformée en énergie. Le sens inverse est aussi possible. On suppose que c’est ce qui s’est passé lors du Big–Bang.

e ⁺

Énergie E

e ˉ

E = m_eˉ . c² + m_e₊ . c² + T_eˉ + T_e₊

= 2 m_e . c² + T_eˉ + T_e₊ E > 2 m_e . c²

= 1,022 MeV

Cet effet est dit « à seuil » : il faut au minimum d’ 1,022 MeV d’énergie

Photons : Eg₁ Eg₂

( e⁺ ; eˉ de la matière)

e ⁺ Ralentissement

Énergie E

e ˉ

E_Détectée = T_eˉ + T_e₊

= E – 2 . 511 keV

N (E_D) = N fois que l’on

détecte telle énergie

Aucun photon perdu *

1 photon perdu *

2 photons perdus *

511 keV

2 . 511 keV

E_Détectée

* : dans le détecteur.

Ø Réaction nucléaire :

Il s’agit d’interactions photon – noyau mais elles sont marginales (rares)

Photon g + ( A ; Z ) Þ Neutron n + ( A –1 ; Z )

Par exemple : les atomes de Carbone et d’Oxygène :

Photon g + ¹²₆C Þ Neutron n + ¹¹₆C (émetteur b⁺ )

Photon g + ¹⁶₈O Þ Neutron n + ¹⁵₈O

N₀ x N(x) = N₀ . exp(–µ.x)

µ = µ_PE : la probabilité d’interaction par effet photo–électrique,

+ µ_C : la probabilité d’interaction par effet Compton,

+ µ_Mat : la probabilité d’interaction par matérialisation,

+ µ_Nucl : la probabilité d’interaction nucléaire (négligeable)

Ø Évolution des probabilités :

§ Évolution de la probabilité d’interaction par effet Compton :

Les interactions par effet Compton (et donc leur probabilité) augmentent avec la densité du matériau.

On rappelle qu’il s’agit de réactions avec les électrons de la matière et que la densité augmente avec le nombre d’atomes dans le matériau.

La probabilité d’interactions par effet Compton diminue quand l’énergie augmente.

µ_C est proportionnelle à 1/E

§ Évolution de la probabilité d’interaction par effet photo–électrique :

Les interactions par effet photo–électrique (et donc leur probabilité) dépendent de la densité du matériau, de l’énergie et de la charge Z des éléments.

On rappelle qu’il s’agit de réactions avec les électrons de la matière et que la densité augmente avec le nombre d’atomes dans le matériau.

La probabilité d’interactions par effet photo–électrique diminue quand l’énergie augmente.

Densité . (charge Z des éléments) ^{^3}

µ_EP est proportionnelle à

Énergie E ^{^2}

C'est–à–dire :

- µ_EP & avec & de la densité,

- µ_EP &&& avec & de la charge Z des éléments,

- µ_EP (( avec & de l’énergie,

§ Évolution de la probabilité d’interaction par matérialisation :

Il s’agit d’interactions à effet seuil : leur probabilité est nulle pour une énergie inférieure ou égale à 1,022 MeV.

La probabilité d’interaction par matérialisation augmente avec l’énergie, avec la charge Z des éléments et avec la densité.

§ La courbe d’évolution est pour un matériau donné (charge et densité données) :

511 keV 1,022 MeV

- À basse énergie, bien inférieure à 511 keV :

" Il y a une dominance de l’effet photo–électrique. et non une exclusivité !

- À moyenne énergie, aux alentours de 511 keV :

" Il y a une dominance de l’effet Compton.

- À haute énergie, supérieure à 1,022 MeV :

" Il y a une dominance de la matérialisation.

Pour un matériau, on détermine sa densité, et son épaisseur moitié. Elle est l’épaisseur pour laquelle N₀ est diminué de moitié et on la calcule par : log(2) /µ .

v Interactions particules chargées – matière :

- Électrons (les plus importants car ils sont mis en mouvement à chaque fois qu’il y a une interaction avec des photons)

- Protons,

- Les particules alpha,

- Les ions lourds.

Ø Interactions électrons – matière :

§ Collision :

Il s’agit d’une interaction coulombienne entre un électron « projectile » (en mouvement) et un électron « cible » (de la matière)

T ; P

1 e²

F = .

4. π . e₀ d²

Cette interaction est répétée avec d’autres atomes et leur cortège électronique jusqu’au ralentissement et l’arrêt de l’électron projectile.

Le paramètre b correspond à la distance des 2 particules s’il n’y avait pas de déviation.

Des échanges d’énergie y sont associés (dans les cas limites) :

b :	0	¥
DT :	troponine	0
Probabilité :	0	¥

La gravité des dégâts est relative à la quantité de ces dégâts sur une petite zone.

Elle est caractérisée par une dose efficace : H = D . Q exprimé en Sievert (Sv)

Q : facteur de qualité sans unité.

Elle correspond à l’intégration de la gravité des dégâts.

Le Sievert est l’unité MKSA, mais on utilise encore le rem. On retrouve la même correspondance entre le Sievert et le rem qu’entre le Gray et le rad :

1 Sievert = 100 rem

1 Gray = 100 rad

La valeur du facteur de qualité Q est en lien avec le transfert linéique d’énergie (TEL) exprimé en MeV.cm_EAU^–1 :

Particules	Facteur de qualité Q	TEL en MeV.cm_EAU^–1
Photons X et g	1
Électrons d’énergie supérieure à 300 keV	1	2
Électrons d’énergie supérieure à 30 keV	1	2,5
Électrons d’énergie inférieure à 300 keV	1,7	5,7
Neutrons lents	3	12
Neutrons rapides	10	53
Protons	10	53
Particules a	20	175
Ions lourds	20	175

Plus le facteur de qualité Q augmente, plus le transfert d’énergie augmente aussi (mais ce n’est pas linéaire pour autant)

Ø Synthèse :

Grandeur	Symbole	Unité SI	Unité pratique	Correspondance
Activité	A	Becquerel (Bq)	Curie (Ci)	1 Ci = 3,7 . 10¹⁰ Bq
Fluence	f	Particules.m^–2	Particules.cm^–2	1 cm² = 10⁴ m²
Débit de fluence	f°	Particules.m^–2.s^–1	Particules.cm^–2.s^–1	–
Énergie	E	Joules ( J )	MeV ou eV	1 MeV = 1,6 . 10^–13 J
Dose absorbée	D	Gray (Gy)	Rad	1 Gy = 100 Rad
Débit de dose	D°	Gy.s^–1	Rad.h^–1	1 Gy.s^–1 = 36 .10⁴ Rad.h^–1
Équivalent de dose	H	Sievert (Sv)	Rem	1 Sv = 100 Rem
Débit d’équivalence de dose	H°	Sv.s^–1	Rem.h^–1	1 Sv.s^–1 = 36 .10⁴ Rem.h^–1

v Calcul de dose :

Ø Particules indirectement ionisantes (photons et neutrons) :

§ Les photons :

N(x) = N₀ . exp^–^m^x

Nombre d’interactions : N_I = N(x) – N₀ = N₀ . (1 – exp^–^m^x)

On calcule la dose maximale en considérant de façon excessive que tous les photons, qui ont interagi, ont déposé toute leur énergie.

C’est vrai pour l’effet photoélectrique mais pas forcément pour l’effet Compton et la matérialisation...

D_Max = E_Max/M

D_Max = N_I . E /M mais : D_Réel < D_Max

Dans l’expression de D, on va retrouver :

- µ_EN (cm^–1),

- E (MeV),

- f (cm^–2)

" MeV.cm^–3 Or la dose est en MeV.g^–1,

il faut la densité r (g..cm^–3)

µ_EN . E . f

D = Mais les unités ne sont pas dans le Système International.

Il faut une conversion :

µ_EN (cm^–1) . E (en MeV) . f (cm^–2)

D = 1,6 . 10^–10 .

r (g.cm^–3)

On simplifie la formule :

- Pour un tissu biologique : on prend r = r_EAU = 1 (au lieu de 0,98) Ça va...

- Pour tout photon dont l’énergie est supérieure à 60 keV (donc quasiment tous) :

on prend µ_EN = 3 . 10^–2 cm^–1

- f = nombre de photons . cm^–2 n’est pas connu, par contre on connaît l’activité de la source (en Becquerel ou en Curie) : A = nombre de photons . s^–1

f° = A /(4 . π . R²) en nombre de photons . m^–2 . s^–1

Il n’est pas anodin de prendre l’activité en Curie : on enlève un 10¹⁰ !

3 . 10^–2 . E (MeV) . A (Ci) . 3,7 . 10¹⁰

D° = 3600 . 1,6 . 10^–10 .

(Gy.h^–1) 1 . 4 . π . R² (m²)

Activité par heure

E (MeV) . A (Ci) . P

D = 0,54 . 1 Gy = 100 Rad

(Rad.h^–1) R² (m²)

" Il est plus simple de diviser par 2 que multiplier par 54…

Avec l’activité, ce que l’on vient de calculer est le nombre de désintégration subies par une source.

Mais…

Toutes les désintégrations n’émettent pas des photons :

Cs

94,6 %

bˉ

5,4 % Ba*

g eˉ

89 % 11 %

Ba

P = 0,946 . 0,89 = 0,81

Pour 100 désintégrations, il y a 81 photons g.

P est le rapport d’embranchement.

Les radiations subies lors des TPs :

On utilise une source ¹³⁷Cs d’activité A₀ = 5 µCi achetée en 2000 et ayant une demi vie de 30 ans.

L’activité A en 2005 = A₀ . e^–^l^.^t = A₀ . e^{–
( Ln2.}^{t )/ t½} = 4 µCi

À une distance de 1 m : Dg = 0,54 . 4 . 10^–6 . 0,662 . 0,81

= 10^–6 Rad.h^–1

= 10^–2 µGy.h^–1

À une distance de 10 cm : Dg = 1 µGy.h^–1

Lors du TP, on est en moyenne à 1 m de la source pendant 3 heures : Dg = 3 . 10^–2 µGy . h^–1

C’est grave docteur ?

La référence en terme de radioprotection :

Pour les professionnels les plus exposés, la dose maximale annuelle est de 20 mSv par an.

Si on ramène cette dose annuelle à l’heure de travail (on en considérait 2000 avant les 35 heures), on arrive à une dose horaire de 25 µSv . h^–1 soit 25 µGy . h^–1.

Alors, avec notre pauvre petit 3 . 10^–2 µGy . h^–1…

… On rigole !

Exemple : le Cobalt

Il y a une descente en cascade et différentes possibilités de désintégrations avec des photons d’énergies différentes.

Il y a une « voie » principale de désintégration proche de 100 %. Les autres sont de l’ordre de 0,00…% et sont donc négligeables.

Dg = (0,54 . A . E₁ . P₁) + (0,54 . A . E₂ . P₂) / d² E₁ = 1,17 MeV E₂ = 1,33 MeV

Mais comme P₁ ~ P₂ ~ 100 %

Dg = (0,54 . A . (E₁ + E₂) / d²

Il existe différentes façons de calculer les doses dont l’utilisation de courbes appelées abaques.

Ces abaques ont pour abscisse l’énergie des particules émises, et pour ordonnée soit une dose, soit un équivalent de dose.

Autre cas :

X

P₁

P₂ B*

g₁ ; E₁

C* B

g₂ ; E₂

C

D(g₁) + D(g₂) Rien ne change car l’activité A correspond à celle des noyaux de départ.

= (0,54 . A . E₁ . P₁) + (0,54 . A . E₂ . P₂) / d²

§ Les neutrons :

Ce que l’on vient de dire est applicable pour les neutrons à une adaptation près :

N(x) = N₀ . e^–^m^x = N₀ . e^–ⁿ^*^r^x ( m = n^* . s )

On observe un plateau de 1 MeV à 100 MeV.

" 7 neutrons par cm² et par seconde correspondent à 1 milli rem par heure.

Ø Particules chargées :

Ces interactions sont toujours présentes car il s’agit d’interactions avec les électrons de la matière.

Elles correspondent à une perte d’énergie dans la matière de ces particules caractérisées par le pouvoir d’arrêt d’une seule particule par unité de longueur.

Pour une dose, il va y avoir :

- Le pouvoir d’arrêt d’une particule en MeV.cm^–1,

- Le flux : le nombre de particules envoyées par la source en cm^–2,

- La masse volumique du matériau en g.cm^–2.

(MeV.g^–1)

D = f . S / r

(Joules.kg^–1)

D = 1,6 . 10^–10 . f . S / r

Ici, le problème qui se pose est de connaître le S (pouvoir d’arrêt)

Formule pratique pour les électrons d’énergie supérieure à 300 keV et pour une distance de 10 cm :

Pour cette formule, on se limite aux électrons : il n’est pas possible de mettre toutes les particules dans le même panier.

Le pouvoir d’arrêt, S, est égal à 2 MeV.cm^–1 (pour l’eau : r = 1g.cm^–1 )

pour une énergie incidente entre 300 keV jusqu’à de très grandes énergies.

D = 1,6 . 10^–10 . f . S / r

(Gray) Avec : r = A / (4 . p . d²)

Débit de dose à 10 cm = D » 3 330 . A (Curie) . P

(rad.h^–1)

Soit on utilise ce calcul, soit on utilise une abaque.

Pour toutes les autres particules chargées, notamment les particules a, on doit utiliser la formule classique.

Mais cela ne pose pas trop de problème car, en général, ces particules sont stoppées dans l’air. Un risque n’est présent que si on est en contact direct de la source.

v Les normes fondamentales :

Ø Historique :

Très tôt après la découverte de ces rayonnements, il y eu la création d’un comité international ayant pour mission de formuler des recommandations sur la protection (1950)

En 1950, ce comité devient le CIPR (Commission Internationale de Protection Radiologique)

Son rôle est de protéger les individus exposés, pas par le biais de lois à cause de son caractère international, mais par le biais de recommandations sur l’observation des personnels directement exposés

(chercheurs, médecins, armée, les populations d’Hiroshima et de Nagasaki, l’exposition naturelle de faibles doses, les animaux de laboratoire, etc.)

Ø Principe :

Le but est la protection des individus, leur descendance et plus globalement le genre humain.

Ø Moyens :

- On réclame une justification de l’utilisation de radioéléments pour le personnel. C’est déjà un peu plus délicat pour la médecine avec les techniques de traitement et de diagnostics.

- Exemple : Le TEP consiste en une injection d’émetteurs b⁺. Il faut justifier son utilisation et savoir si une autre technique n’aurait pas pu la remplacer comme l’échographie, la Résonance Magnétique Nucléaire

(mais, pour la RMN, il n’y a pas beaucoup d’appareil en France donc on soumet des patients à des rayonnements alors que l’on pourrait parfois faire autrement)

- On optimise la radioprotection. Si on soumet quelqu’un à un rayonnement, il faut qu’il soit le plus faible possible avec l’utilisation de filtres (pour le patient et aussi pour le manipulateur)

- On fixe la dose à des valeurs limites et classifie les effets en 2 catégories.

Les effets non aléatoires	Les effets aléatoires
Ce sont des effets déterminés pour une dose déterminée. Ils sont dits « à seuil » : on est en mesure de voir les conséquences immédiates ou presque (1 heure, 1 jour, etc.) Il s’agit d’effets précoces.	Ils sont régis par une probabilité d’apparition en fonction de la dose reçue. Ils ne présentent pas de seuil. Ce sont des effets tardifs.
La norme = le seuil Ils sont faciles à gérer : on se met en dessous de ces doses et on ne risque rien.	Les normes = les chiffres limites où la probabilité est « acceptable »
Exemples : - Altération de la formule sanguine Rougeurs de la peau « coup de soleil », - Chute des cheveux (aussi une cause chimique), - Dermite, - Cataracte : usure et opacification du cristallin (naturelle chez les personnes âgées) prématurées par les rayonnements ionisants, - Atrophie, - Stérilité, - Etc.

Ø Valeurs pratiques des normes :

§ Effets non aléatoires :

Une limite de dose H_L est 500 mSv pour tous les tissus. Sauf le cristallin, elle est fixée à 150 mSv.

§ Effets aléatoires :

Il va falloir gérer un risque (développement de cancer) On définit le risque d’apparition de cancer pour une quantité reçue de rayonnement donné (c’est–à–dire pour une dose donnée)

Le risque est différent entre les hommes et les femmes.

" Le nombre de cancers observés par Sievert de dose reçue :

Pour les matériaux semi–conducteur, le gap est d’environ 1 eV.

Niveau donneur dans la Bande interdite (BI)

« Gap »

Niveau accepteur dans la Bande interdite (BI)

Ce type de matériau est difficile à manipuler (refroidissement du matériau dans l’azote) mais offre une très grande qualité de mesure.

Ø Processus d’excitation :

§ Scintillateurs :

NAI (matériau transparent ressemblant au plexiblas)

Aluminateur (un noir absolu est nécessaire pour ne pas avoir d’interactions avec l’éclairage de l’extérieur)

PM : Photomultiplicateur (cellules photo–électriques pour transformer la lumière en électricité)

1 photon g " 1 électron " 10⁴ photons visibles " 10² électrons " PM

Les scintillateurs organiques dépendent des propriétés intrinsèques de la molécule indépendantes de son état solide ou liquide (cristaux, liquides, plastique)

Absorption Phosphorescence

d’énergie Fluorescence (lent)

(rapide)

Les scintillateurs inorganiques correspondent à peu près à des détecteurs semi–conducteurs avec ou sans activateur (exemple : NAI, CSI)

État excité de l’activation : création de niveau d’énergie dans la zone de bande interdite.

État fondamental.

Le tube PM constitue une structure multiplicatrice où on observe un phénomène de cascade (cf TD)

La largeur à mi–hauteur est due à la qualité plus ou bonne du détecteur.

(plus la qualité augmente, plus la largeur à mi–hauteur diminue)

662 keV (où toute l’énergie est transférée)

Ø Transformation physico–chimique :

§ Exemple de l’émulsion photographique :

Électron

H₂ = H ∙ — ∙ H " H ∙ ; H ñ

Photon

On utilise un support de gélatine et d’ions Bromure–Argent. Ces ions deviennent des atomes d’Argent, des traces qui noircissent par révélation et déterminent la quantité d’ionisation.

§ Détecteur solides de traces :

Ils sont basés sur le même principe.

" Le rayonnement transforme les matériaux et les fragilise. On produit alors des agressions chimiques (comme avec l’acide) formant alors des micro–trous aux endroits fragilisés.

On compte alors ces trous à l’aide d’un microscope.

On peut diriger notre plus grande admiration

aux scientifiques qui emploient cette technique !

Origine des rayonnements

Processus atomique

v Atome Hydrogène, modèle de Bohr :

Quand on soumet un atome d’Hydrogène à une décharge électrique, on observe des raies à des longueurs d’onde précise.

Personne ne comprend pourquoi…

Ø D’un point de vue mécanique :

On sait gérer un mouvement circulaire et une force d’attraction (force coulombienne)

1 e ²

F_n = . . n avec n , un vecteur unitaire.

4. π . e₀ r ²

La somme des forces est égale à l’accélération : S F = m . g

Pour un mouvement circulaire : g = v² / r

1 e ² v

. = m . g = m . v² / r n

4. π . e₀ r ²

1 e ²

. = m . v²

4. π . e₀ r

L’énergie d’un électron :

E_TOTALE = E_CINETIQUE + E_POTENTIELLE

E_C d’une particule classique = y m v²

E_P = ?

Soit une craie posée sur une table avec une énergie de référence :

Au repos Toujours au repos mais elle

(énergie de référence) présente une énergie potentielle.

E_P = m . g . h

Mais pour l’électron : quelle est l’énergie de référence ?

E_P = 0 si r " ¥

E_P = _¥^r¦ F_n dx = _¥^r¦ 1/(4.π.e₀) . e² . dx / x²

= e² /(4.π.e₀) . [–1/x]^r_¥ = e² /(4.π.e₀) . [–1/_¥ – (–1/r]

= 0

= e² /(4.π.e₀) . 1/r

E_T = E_C + E_P = y m v² + e²/(4.π.e₀) . 1/r

= y 1/(4.π.e₀) . e²/r – 1/(4.π.e₀) . e²/r

E_T = – y 1/(4.π.e₀) . e²/r =

E_T = f(r) avec r allant de 0 à ¥.

Alors pourquoi des longueurs d’ondes précises ?

Énergie de liaison d’un système :

E_P + E_C = E_T(i)

On suppose qu’ils sont à une distance r = ¥

et qu’ainsi ils sont au repos :

v = 0 E_C = 0 Et comme r = ¥ , E_P = 0

Donc E_T(f) = 0

E_Liaison + E_T(i) = E_T(f)

E_L = E_T(f) – E_T(i) = – E_T(i) = y 1/(4.π.e₀) . e²/r

Cela supposerait que l’électron de l’atome H pourrait avoir toutes les énergies possibles.

Or expérimentalement, c’est faux à causes des longueurs d’onde précises.

Ø Postulats de Bohr :

Beaucoup de bidouilles…

§ 1^er postulat : postulat mécanisme :

Il fixe des moments cinétiques s = n.h avec s = m.v.r et h = h/2p h = 6,62 . 10^–34 J.s^–1

n N

On entre dans la mécanique quantique…

m.v² = 1/(4.π.e₀) . e²/r et s = n.h = m.v.r donc v = n.h /(m.r)

Donc m.n².h² /(m.r)² = 1/(4.π.e₀) . e²/r

On fige alors r : r = n².h² /(m. e²) . 4.π.e₀ et r = n².r₀

Avec r₀ = h² /(m. e²) . 4.π.e₀ = 0,53 Å

E_T = – y 1/(4.π.e₀) . e²/r

E_T = – y [1/(4.π.e₀)]² . e⁴.m /(n².h²)

E_T = – y [1/(4.π.e₀)]² . e⁴.m /h² . 1/n²

E_T = – E₀ /n² avec E₀ = 13,6 eV

E_n = – E₀ /n² r_n = n².r₀ r₀ = 0,53 Å (n=1)

§ 2^ème postulat : postulat optique :

L’électron peut se déplacer entre les différents états d’énergie accessibles. n N

(n=1) (n=2) (n=3) (n=4)

E_n = –13,6 eV ; –13,6/4 ; –13,6/9 ; –13,6/16

État initial i " État final f

Ei Ef

Si Ei < Ef, l’électron absorbe de l’énergie (= Ef – Ei)

Si Ei > Ef, l’électron émet de l’énergie (= Ei – Ef)

Transitions :

L’électron va de n=4 à n=1. E₄ = –13/16 E₁ = –13 eV

E = E₄ – E₁ = 13,6 (1 – 1/16) = 15/16 . 13,6

" Possible pour toutes les transitions (avec tous les états)

E = Ei – Ef = – E₀ ( 1/n_i² – 1/n_f²) (= énergie émise)

Voir le site http://www.physique–eea.unicaen.fr/~tice/coursenligne.html " Atome de Bohr

Absorption d’énergie par l’atome :

La structure atomique peut stocker de l’énergie par un changement du niveau d’énergie de l’électron.

Mais il faut apporter l’énergie correspondant précisément à un état possible pour l’électron.

Si on apporte une énergie entre E_n et E_n+1, rien ne se passe.

Si on apporte une énergie supérieure à l’énergie de liaison E_L, l’électron quitte l’atome. On parle d’ionisation de l’atome.

L’apport d’énergie peut se faire par une décharge électrique ou par des photons.

Tout élément tend vers son état fondamental.

Quand l’électron est sur une couche différente que sa couche fondamentale, il y retourne en libérant son surplus d’énergie par un quantum (= photon) d’énergie.

Pour l’atome de Bohr, l’état fondamental de l’électron est n=1 et correspond à l’énergie de liaison maximale avec l’atome.

L’électron a la possibilité de passer de l’état n à l’état fondamental directement ou par une cascade jusqu’à l’état fondamental.

Les photons libérés ont une longueur d’onde différente en fonction des différences d’énergie entre les états.

Toutes les transitions d’un état n>2 vers n=2 (= série de Balmer) ont pour conséquence l’émission de photons avec des longueurs d’ondes dans le domaine du visible.

v Généralisation aux atomes hydrogénoïdes :

Ils ressemblent à l’Hydrogène (= avec un seul électron)

" § H ; ¸ He⁺ ; ⁶₃ Li²⁺ ; etc ; ²⁰⁸₈₂ Pb⁸¹⁺

(on sait le faire)

Pour l’atome de Bohr :

F = 1/(4.π.e₀) . e²/r²

Pour un atome hydrogénoïde :

F = 1/(4.π.e₀) . Z . e²/r²

E_n = – E₀ . Z² /n²

v Généralisation à tous les atomes :

Les autres électrons font écran

au noyau.

F = 1/(4.π.e₀) . Z_Eff . e²/r²

F = 1/(4.π.e₀) . (Z–s_e) . e²/r²

Avec s_e = constante d’écran des autres électrons.

E_n = – E₀ . (Z–s_e)² /n²

√(E_n) est proportionnel à Z √(E_n) = √(– E₀ /n²) . Z – s_e

Cette démarche est bonne au point de vue de l’énergie mais pas au point de vue de la localisation.

La position de l’électron n’est pas définie mais seulement une fonction d’onde Y(x, y, z, t) telle que la probabilité de trouver l’électron entre x et x+dx ; y et y+dy ; z et z+dz et entre t et t+dt correspond à dP = |Y(x, y, z, t)|² dx dy dz dt

La position de l’électron n’est pas définie sur une sphère parfaite avec un rayon précis. On peut trouver un électron partout dans l’espace ; la probabilité dP n’est donc jamais nulle.

Ø Modèle de Bohr Summerfeld :

n : nombre quantique principal

l : nombre quantique orbital (= rapport grande orbite/petite orbite)

m : nombre quantique magnétique (angle entre l’horizontale et le grand axe)

s : nombre quantique de spin (rotation de l’électron sur lui–même)

Quand n augmente, l’énergie E augmente et l’énergie de liaison E_L diminue.

Pour un n donné :

Quand l augmente, l’énergie E augmente et l’énergie de liaison E_L diminue.

L’état d’un électron est donné par n, l, m_L et m_S. Exemple : n=1 l=0

L’état fondamental correspond à l’état d’énergie de liaison maximale (= état le plus stable)

§ Tableau de Mendeleïev :

Nombres quantiques				Sous–couche	Couche	Nb d’électrons dans la sous–couche	Nb total sur la couche
n	l	m_L	m_S	Sous–couche	Couche	Nb d’électrons dans la sous–couche	Nb total sur la couche
1	0	0	+/– y	1 s	K	2	2
2	0	0	+/– y	2 s	L	2	8
2	1	–1 0 1	+/– y	2 p	L	6	8
3	0	0	+/– y	3 s	M	2	18
	1	–1 0 1	+/– y	3 p		6
	2	–2 –1 0 1 2	+/– y	3 d		10
4	0	0	+/– y	4 s	N	2	32
	1	–1 0 1	+/– y	4 p		6
	2	–2 –1 0 1 2	+/– y	4 d		10
	3	–3 –2 –1 0 1 2 3	+/– y	4 f		14

Le nombre total d’électrons par couche : N_T = 2n²

On ne peut pas avoir 2 électrons avec les mêmes nombres quantiques n, l, m_L et m_S.

§ Organisation en énergie :

" Couplage spin – orbite.

j = l + s

| l – s | < j < | l + s |

j = l + s

j = l – s

n=1	l=0	s=+/– y	j = y	Une seule valeur d’énergie	K
n=2	l=0	s=+/– y	j = y	Une seule valeur d’énergie	L_I
n=2	l=1	s=+/– y	J = y ; ”	2 valeurs d’énergie	L_II et L_III
n=3	l=0	s=+/– y	j = y	Une seule valeur d’énergie	M_I
	l=1	s=+/– y	J = y ; ”	2 valeurs d’énergie	M_II et M_III
	l=2	s=+/– y	j = ” ; 5/2	2 valeurs d’énergie	M_IV et M_V

3 énergies

différentes

Exemple : ⁶₃ Li

L_III

L_II

L_I

État État État

fondamental excité ionisé

v Absorption et émission d’énergie par la structure atomique :

Ø Absorption :

§ Excitation :

L_III

L_II

L_I

État fondamental État excité

L’énergie apportée est exactement : E = E_L_III – E_K

De plus, il faut que la sous–couche L_III ne soit pas déjà occupée par des électrons.

Ce processus peut permettre des réactions chimiques, dites photo–induites (= excitation par des photons)

§ Ionisation :

L’énergie apportée : E ≥ E _l_K

E = E _l_K + T_eˉ

Ø Émission :

§ Fluorescence :

Point de départ : État excité (voire ionisé)

E = E_L_III – E_K

= E _l_K – E _l_L_III

Rayon X

⁶₃ Li*

E_X1

E_X2

E_X

Rayon X

E_X3

E = – E_K = E _l_K

E _l_K = E_X1 + E_X2 + E_X3 E_X1 = E _l_M_V ; E_X2 = E _l_L_III – E _l_M_V ; E_X3 = E _l_K – E _l_L_III

§ Nomenclature des transitions électroniques donnant les raies X les plus intenses :

L_a₁ L_a₂ L_b₁ L_b₂

K_a₁ K_a₂ K_b₁ K_b₂

On établie une table d’énergie pour tous les éléments.

Loi de Moseley :

√(E_K_a₁)

(en keV)

" Droite presque parfaite

№ atomique

v Interaction rayonnement – matière :

Ø Application :

La lumière blanche :

Il s’agit d’un mélange de toutes les radiations :

Bleu : 480 nm

Cyan : 500 nm Magenta : 720 nm

Vert : 530 nm Rouge : 700 nm

Jaune : 590 nm

Exemple : La chlorophylle absorbe le magenta, on voit donc la couleur verte.

La vision nocturne :

Elle est possible grâce à la sensibilité des cellules à bâtonnet.

Sensibilité relative 5100 Å 5550 Å

(arbitraire)

Vision nocturne (cellules à bâtonnets)

= Sensibilité aux bleus

Vision diurne (cellules à cône)

= Capacité de supporter de grandes variations

d’intensité de la lumière.

" peu de sensibilité dans les bleus

et une grande finesse dans le rouge.

La longueur d’onde 5550 Å correspond à la couleur verte " les lunettes de soleil ont un reflet vert.

Le soleil et la peau :

Le soleil émet des longueurs d’onde de 3 000 Å et 50 000 Å. Entre le soleil et nous, il y a l’atmosphère qui filtre.

Intensité à la surface : UV : 8 % entre 0,2 µm et 0,4 µm

Visible : 41 % entre 0,4 µm et 0,4 µm

IR : 51 % entre 0,7 µm et 5 µm

Intensité

Sensibilité de la peau

Spectre du soleil au zénith

Tout petit domaine en longueur d’onde

qui fait réagir la peau (rougeurs)

" Protection par une crème.

l (en µm)

0,28 0,3 0,32 0,34 0,36

L’épaisseur de la couche d’atmosphère va jouer sur le filtrage (différence aussi entre le niveau de mer et l’altitude)

Le laser :

(Light Amplification by Stimulated Emission Radiation)

Il est souvent utilisé dans des applications médicales. Il est basé sur le principe du stockage d’énergie dans les structures atomiques et en la concentration de cette énergie.

Un électron va de la couche K vers une couche supérieure par excitation. Celui–ci va retomber de la couche M à K, lors de la réorganisation atomique, avec l’émission d’un photon.

Pour le laser, on utilise des matériaux tels que la retombée se fasse sur le niveau 2 (niveau métastable) pendant quelques millisecondes.

Il y a alors un fort peuplement d’électrons dans ce niveau. On parle d’inversion de population du niveau 1 au niveau 2.

On éclaire ensuite ces atomes ayant cette configuration avec des photons d’énergie E = E₂ – E₁.

Il y a une retombée des électrons du niveau 2 au niveau 1, avec 2 fois plus de photons d’énergie E = E₂ – E₁.

Il s’agit d’un stockage de l’énergie et de sa libération instantanée sous forme lumineuse. De plus, une direction fine du faisceau est possible.

Son utilisation :

- Show laser en discothèque,

- Applications médicales :

- Chirurgie fine (soudure de petit vaisseaux sanguins),

- Stérilisation (pas de contact avec les instruments),

- Choix des réactions (avec le choix de couleur),

- Chirurgie avec incision fine avec une diminution de la douleur,

- Etc.

- Opthalmologie (avec un laser excimètre : UV) :

- Décollement de la rétine,

- Défaut de vision par la modification de la forme de la cornée,

- Etc.

- Détatouage (dissociation des molécules d’encre),

- Etc.

Origine des rayonnements

Processus nucléaire

v Le noyau :

Ø Description rapide :

- Sa taille est de l’ordre du Fermi (10^–15 m) de 1 à 10 fm.

" La taille de l’atome est de l’ordre de l’angström (10^–10 m)

- Sa masse constitue plus de 99 % de la masse de l’atome.

- Les forces qui y sont exercées sont des répulsions coulombiennes entre les protons. Pour les contrecarrer, il faut une force colossale : la force nucléaire.

Le noyau radioactif est un noyau instable. Le terme d’ « atome radioactif » est mal adapté puisqu’il s’agit plus particulièrement du noyau.

La radioactivité est le seule transformation qui se fait toute seule.

Ø Nomenclature :

§ Noyau :

A : nombre de nucléons (= nombre de masse) 1 uma = 1 masse d’un nucléon

Z : nombre de protons (= de charge) = nombre d’électrons (pour un atome neutre)

" Il permet la définition d’un élément chimique.

N : nombre de neutrons = A – Z

Exemple : L’élément Iode 53 protons " ₅₃I

et différents nombre de neutrons (127, 129, 131, 132, etc.)

" Définition des différents isotopes de l’Iode.

Carte des noyaux :

Z N = Z

(jamais observés,

mais recherchés)

Zone (ou vallée) de la stabilité

(environ 300 noyaux sur 3 500 étudiés)

Plus on s’éloigne de la vallée de stabilité, plus les noyaux sont instables et plus leur durée est courte.

On peut considérer que tous les noyaux sont radioactifs, mais avec des durées de vie plus ou moins longues.

Pour un noyau lourd, il y a une perte de matière avec l’émission d’une particule ¸a

(= noyau d’Hélium : pas d’électron !!)

N = Z

Même nombre Z

= isotopes

Vallée de stabilité

Même masse

= isomère

Même nombre de N

= isotones

§ Réactions nucléaires :

Il s’agit du passage (ou transformation) d’un état initial « i » à un état final « f ».

Diffusion élastique : « i » Û « f » Exemple :

Diffusion inélastique : « i » ¹ « f » Exemple :

a + A " b + B

Bilan énergétique : Q = m_a.c² + m_A.c² – m_b.c² – m_B.c²

= c² (m_a+ m_A – m_b – m_B)

" Le bilan énergétique consiste en fait en un bilan de masse.

Q > 0 : m_i > m_f " Production d’énergie

(souvent sous forme d’énergie cinétique des produits)

= réaction exothermique.

Q < 0 : m_i < m_f " Apport d’énergie cinétique par les réactifs

et consommation de cette énergie

v Énergie de liaison des noyaux :

¿ X " Z . p + (A–Z) . n

L’énergie de liaison E, E _l_A–Z ,est nécessaire pour éclater un noyau en Z protons et (A–Z) neutrons.

Comment la calculer ?

m_x.c² + E _l_A–Z = Z . m_p.c² + (A–Z) m_n.c²

E _l_A–Z = Z . m_p.c² + (A–Z) m_n.c² – m_x.c²

On a besoin de connaître m_x (= la masse du noyau X) Or, on ne connaît que M_x (= masse de l’atome, donnée dans les tables)

Atome X " noyau X + Z . m_eˉ

M_x.c² + E _l_Z_e = m_x.c² + Z m_e.c²

m_x.c² = M_x.c² + E _l_Z_e – Z m_e.c²

Pour l’Hydrogène : (1 proton et 1 électron) m_p.c² = M_H.c² + E _l₍_e_H) – m_e.c²

E _l_A ;
Z = Z.M_H.c² + Z.E _l_Z_e – Z.m_e.c² + (A–Z) m_n.c² – M_x.c² – E _l_Z_e + Z m_e.c²

E _l_A ;
Z = Z.M_H.c² + (A–Z) m_n.c² – M_x.c² + Z.E _l_Z_e – E _l_Z_e

E _l_A ;
Z /A = énergie moyenne par nucléon

Le noyau le plus stable est le Fer.

" Il a la plus forte énergie par nucléon.

Fusion Fission symétrique

¹⁶O ²⁶Fe ⁵⁴Xe ²³⁴U

Noyau lourd " 2 noyaux légers

_Z^AX " _Z1^A1X₁ + _Z2^A2X₂ A = A₁ + A₂ ; Z = Z₁ + Z₂

M_x.c² = M_x₁.c² + M_x₂.c² + DE

DE = M_x.c² – M_x₁.c² + M_x₂.c²

= Z.M_x.c² – (A–Z).m_n.c² + E _l_{A ; Z} + E _l_A₁_{; Z}₁ – Z.M_x.c² – (A₁–Z₁).m_n.c² + E _l_A₂_{; Z}₂ + Z.M_x.c² – (A₂–Z₂).m_n.c²

DE = E _l_A₁_{; Z}₁ + E _l_A₂_{; Z}₂ – E _l_{A ; Z}

DE = A₁.E _l_A₁_{; Z}₁ /A₁+ A₂.E _l_A₂_{; Z}₂ /A₂ – A.E _l_{A ; Z}/A

E _l_A₁_{; Z}₁ /A₁ > E _l_{A ; Z}/A

DE > 0

E _l_A₂_{; Z}₂ /A₂ > E _l_{A ; Z}/A

E _l_A–Z = Z . M_H.c² + (A–Z) m_n.c² – M_A ;
Z.c²

= Dm.c²

" Énergie = Masse Cette formule rappelle celle d’Einstein : E = m.c²

E _l_A–Z correspond à l’organisation (ou configuration) des nucléons dans le noyau.

v Radioactivité :

Pour une énergie E _l_A–Z, il y a un grand nombre de configurations des nucléons possibles.

Soit : n_S : le nombre de configurations stables,

n_IS : le nombre de configurations instables.

Particule a

Sur un temps infini, la probabilité totale de transformer sa configuration = n_IS /(n_S+n_IS)

La constante radioactive l est la probabilité pour un noyau de se désintégrer par unité de temps.

Si l = 0 , le noyau est rigoureusement stable ;

Si l ¹ 0 , le noyau est instable (ou radioactif), c’est–à–dire avec une certaine probabilité de se désintégrer.

Ø Processus de désintégration :

§ Processus a :

Cela concerne les noyaux lourds.

¿ X " ¿^–_–¸ Y* + ¸ a

Cette désintégration entraîne une pagaille dans les nucléons qui restent dans le noyau. Donc celui–ci est sûrement dans un état excité (l’organisation des nucléons n’est pas idéale)

La durée de vie de cet élément excité est très courte (10^–15 s) Il y a des cas où elle est plus longue (supérieure à 10^–9 s) On parle d’état isomère ou métastable (vu avec le laser)

Retour à un état stable :

¿^–_–¸ Y* " ¿^–_–¸ Y + g

Qu’est–ce qui nous intéresse dans ce processus ?

Les particules a sont arrêtées dans l’air ; il n’y a un problème que s’il y a un contact direct avec la peau, en cas d’ingestion ou en cas d’inhalation.

Les photons g sont plus dangereux car ils traversent de grandes épaisseurs d’air.

" Ea ?

Principe de conservation de l’énergie :

M_x.c² = M_Y.c² + M_a.c² + T_a + T_Y + E _Y*

Q_a = M_x.c² – M_Y.c² – M_a.c² = T_a + T_Y + E _Y*

Principe de conservation de la masse : 0 = P_a + P_Y

P_Y

P_a

T = P²/2M P_a = P_Y

Q_a = P_Y²/2M_Y + P_a²/2M_a + E _Y* = P_a²/2M_a (1 + M_a/M_Y) + E _Y*

Q_a = T_a (1 + M_a/M_Y) + E _Y*_.

Mesuré

Donné pour les tables Mesuré Donné pour les tables

§ Processus bˉ :

¿ X " ¿₊₁ Y* + _–₁ bˉ + u

Un neutron est transformé en un proton.

Neutron " Proton + bˉ + 1 antineutrino

N(T_b_ˉ)

Le bˉ peut avoir toutes les énergies possibles

de 0 à T_b_ˉmax à cause de la présence de u dont l’énergie varie

T_b_ˉmax

T_b_ˉ

¿^–_–¸ Y* " ¿^–_–¸ Y + g

§ Processus b⁺ :

¿ X " ¿₊₁ Y* + _–₁ b⁺ + u

Un proton est transformé en un neutron.

Proton " Neutron + b⁺ + 1 neutrino

¿^–_–¸ Y* " ¿^–_–¸ Y + g

Ø Décroissance radioactive :

Le noyau est le seul objet capable de se transformer.

0 t t+dt

Temps

N₀ N(t) N(t+dt)

= ?

dN = N(t+dt) – N(t) = – l . N(t) . dt

dN/N = – l dt " ¦dN/N = ln N

ln N = – l.t + C C = constante

N(t) = e^ln[N(^t^)] = e^–^l^t^{+ C} = e^C . e^–^l^t

N(t) = e^C . e^–^l^t

Détermination de e^C :

N(t=0) = e^C . e^–^l^.⁰

N₀ = e^C

" N(t) = N₀ . e^–^l^t

D l ressemble à la probabilité d’interaction du photon dans la matière : N(x) = N₀ . e^–^µ^x x correspond alors à l’épaisseur de la matière ; alors qu’ici t correspond à l’évolution dans le temps.

Ø Nomenclature :

§ Activité :

Il s’agit du nombre de désintégrations par unité de temps à la date t.

Son unité est le Becquerel : 1 Bq = 1 désintégration par seconde.

1 Ci = 3,7 . 10¹⁰ Bq

Historiquement, 1 Curie correspond au nombre de désintégrations d’un gramme de Radium (Rn) par seconde.

0 t t+dt

Temps

N₀ N(t) N(t+dt)

A₀ A(t) A(t+dt)

A(t) = l.N(t) = l . N₀. e^–^l^t = A₀. e^–^l^t

Avec A₀ : l’activité d’un échantillon à t = 0

§ Période :

Elle correspond au temps au bout duquel la moitié des noyaux se sont désintégrés.

0 T_½

Temps

N₀ N₀/2

N(t= T_½) = N₀/2 = N₀ . e^–^l^T^½

e^–^l^T^½ = y " ln e^–^l^T^½ = – ln 2

l . T½ = ln 2 " T½ = ln 2/l.

troponine	0	T½	2 T½	…	10 T½
N	N₀	N₀/2	N₀/4	…	N₀/1024

À t = n T½ N(t) = N₀ /2ⁿ

N(t = nT½) = N₀ . e^–^lⁿ^.^T^½ = N₀ . e^–^ln2/^T^½ ⁿ^.^T^½

= N₀ . e^–ⁿ^.^ln2 = N₀ . 2^–n = N₀ /2ⁿ

Exemple de Tchernobyl :

Le ¹³⁷Cs dans l’environnement a une période de 30 ans.

De 1986 à 2005, il y a eu 19 ans. Il reste plus de la moitié Césium initial dans l’environnement.

§ Période biologique :

Soit un échantillon liquide avec quelques noyaux radioactifs.

t = 0

N₀

A₀ A₀ (mesurable)

N₀

À une date t : À une date t :

A’(t) A(t)

N’(t) N(t)

A’(t) < A(t)

parce que des noyaux radioactifs se sont échappés de l’individu par la transpiration, les excrétions et les urines.

Dans le bonhomme :

0 t t+dt

Temps

N₀ N(t) N(t+dt)

dN = – l_p . Ndt – l_b . Ndt

l_p : Constante radioactive physique.

l_b : Probabilité pour un noyau radioactif (l’élément chimique correspondant) d’être éliminé par l’organisme.

dN = – (l_p + l_b) . Ndt = – l_effectif . Ndt

Intégration :

N(t) = N₀. e^–^l^effectif^t = N₀. e ^–(^l^p⁺^l^b⁾^t

Application médicale :

L’injection de produits radioactifs dans le sang permet de déterminer le volume du sang par un rapport de dilution (qui se fait en quelques secondes)

Exemple de l’Iode, le rapport de dilution dans le sang est très faible. En effet, quasiment tout l’Iode se fixe dans la tyroïde et donc il est sorti su système sanguin.

Donc si l’on calcule le rapport de dilution dans le sang, il sera faussé et on trouvera quelques centaines de m³.

L’injection de produits radioactifs constitue une contamination ; donc il faut faire attention aux doses.

Exemple : L’élément ¹³¹I :

T_b : 139 jours T_p : 8,04 jours

T_b : la période biologique ; c’est le temps mis par l’organisme pour rejeter la moitié de l’élément (au sens chimique)

T_b = ln 2/l T_p = ln 2/l

Donc l_effective = l_p + l_b = ln2/T_p + ln2/T_b = ln2/T_effective

" ln2/T_effective = 1/T_p + 1/T DEt pas une somme directe !

Ø Filiation radioactive :

A " B " C

Noyau père Noyau fils Noyau petit–fils

(pas forcément (considéré stable

stable) dans notre cas)

Exemple : L’examen médical :

Sur le temps d’étude, il faut que l’on ait un phénomène produit, donnant lieu à une observation médicale.

Souvent :

l_A ; T_A l_B ; T_B

A " B " C

Période longue Période courte

= Réserve (que l’on injecte au patient

chaque jour ou heure)

Il faut connaître : N_A(t) ; N_B(t) et N_C(t)

0 t t+dt

Temps

N₀ N_A(t) N_A(t+dt)

N_B(t) N_B(t+dt)

N_C(t) N_C(t+dt)

À t = 0 :

On suppose que N_A(t=0) = N₀ " Il n’y a que des noyaux A

N_B(t=0) = 0

N_C(t=0) = 0

À une date t quelconque :

N_A(t) + N_B(t) + N_C(t) = N₀

Nombre de noyaux A :

dN_A = – l_A N_A dt " dN_A/N_A = – l_A dt

Intégration : lnN_A = – l_A . t + a

N_A(t) = e^–^l^A^t⁺^a = e^–^l^A^t. e^a N_A(t=0) = N₀ = 1. e^a

N_A(t) = N₀ . e^–^l^A^t

Nombre de noyaux B :

dN_B = l_A N_A dt – l_B N_B dt

Solution partielle : dN_B = – l_B N_B dt " N_B(t) = B₁ . e^–^l^B^t

Solution générale : N_B(t) = B₁(t) . e^–^l^B^t

On accepte que B₁ ne soit pas une constante et dépende du temps pour prendre en compte l_A N_A dt.

On va donc bidouiller B₁ pour qu’elle soit valable tout le temps.

Dérivation de B₁(t) . e^–^l^B^t :

dB₁/dt . e^–^l^B^t + B₁ (–l_B) e^–^l^B^t = B₁ (–l_B) e^–^l^B^t + l_A N₀ e^–^l^A^t

dB₁/dt . e^–^l^B^t = l_A N₀ e^–^l^A^t

" dB₁/dt = l_A N₀ e^–
(^l^A^–^l^B⁾^t

Intégration :

l_A N₀

B₁ = e^{– (}^l^A^–^l^B⁾^t + B₂ avec B₂ = constante

l_B– l_A

N_B(t) = B₁(t) . e^–^l^B^t = (l_A N₀)/(l_B– l_A) . e^–^l^A^t+ B₂.e^–^l^B^t

N_B(t=0) = 0 = (l_A N₀)/(l_B– l_A) . 1 + B₂ . 1

" B₂ = – (l_A N₀)/(l_B– l_A)

N_B(t) = (l_A N₀)/(l_B– l_A) [e^–^l^A^t – e^–^l^B^t]

Nombre de noyaux C :

N_C(t) = N₀ – N_A(t) – N_B(t)

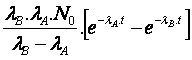Activité :

A_A(t) = l_A N_A(t) = ± l_A N₀ e^–^l^A^t de même : A_B(t) = l_B N_B(t) =

A_C(t) = 0 (les noyaux sont stables)

l_A ; T_A l_B ; T_B

A " B " C

Cas particulier : T_A >> T_B

A_B(t) = l_B (l_A N₀)/(l_B– l_A) [e^–^l^A^t – e^–^l^B^t]

Si T_A >> T_B ; alors l_A << l_B.

Donc il existe un temps t tel que : T_A >> t >> T_B

e^–^l^A^t = e^–^ln2^{t /}^T^A

e^–^l^B^t = e^–^ln2^{t /}^T^B qui tend vers 0

A_B(t) = l_B l_A N₀ /(l_B– l_A) . e^–^l^A^t = l_A N₀ e^–^l^A^t = A_A(t)

négligeable

Autre cas de figure :

Soit T_A et T_B quelconques (avec des valeurs standard)

À t = 0 : N_A(t=0) = N₀

N_B(t=0) = 0

N_C(t=0) = 0

Quand t tend vers ¥ : N_A tend vers 0

N_B tend vers 0

N_C tend vers N₀

On remarque que N_B part de 0 et va vers 0.

Hum hum…

N(t)

N_A(t)

N₀

N_C(t)

N₀/2

N_B(t)

Temps

T_B Tm

N_B(t) = (l_A N₀)/(l_B– l_A) [e^–^l^A^t – e^–^l^B^t]

dN_B(t)/dt = (l_A N₀)/(l_B– l_A) [–l_A. e^–^l^A^t + l_B . e^–^l^B^t]

Pour le temps t = Tm : dN_B/dt = 0

Donc : –l_A. e^–^l^A^Tm = l_B . e^–^l^B^Tm

Tm = 1/(l_B– l_A) . ln( l_A /l_B ) e^–^l^B^Tm = ( l_A /l_B ) e^–^l^A^Tm

A_B(t=Tm) = (l_B l_A N₀)/(l_B– l_A) [e^–^l^A^Tm – (l_A /l_B) e^l^A^Tm]

= (l_B l_A N₀)/(l_B– l_A) . e^–^l^A^Tm [ 1 – (l_A /l_B) ]

= (l_B l_A N₀)/(l_B– l_A) . e^–^l^A^Tm [ (l_A –l_B)/l_B ]

= l_A . N₀ . e^–^l^A^Tm

= A_A(t=Tm)

A(t)

A_A(t)

A₀

N_C(t)

N_B(t) Temps

Pour les filiations des grandes familles de radioéléments, les désintégrations amènent à chaque fois vers le plomb Pb.

Cet élément présente un nombre de nucléons dit « magique » qui le rend très stable.

Matériau	Énergie (en MeV)	DT/Dx collision (en 10^–3 MeV.cm^–1)	DT/Dx freinage (en MeV.cm^–1)	Parcours R
Aluminium r = 2,7 g.cm^–1	0,5	1,58	1,83 . 10^–5	0,83 mm
	5	1,66	1,29 . 10^–4	11,4 mm
	10	1,638	2,82 . 10^–4	21,4 mm
Air r = 1,29 mg.cm^–1	1	1,657	1,76 . 10^–5	3,8 m
	5	1,83	8,12 . 10^–5	22 m
	10	1,97	1,78 . 10^–4	40 m
Eau r = 1 g.cm^–1	1	18,7	1,76 . 10^–5	0,43 cm
	5	19,4	8,20 . 10^–5	2,50 cm
	10	20,3	1,80 . 10^–4	4,80 cm

Particules :	Énergie (en MeV)	Vitesse (en cm.s^–1)		Parcours R (en µm)
Particules :	Énergie (en MeV)	Dans l’eau	Dans l’air	Dans l’eau	Dans l’air
Électron	10^–2	5,8		2,15
	1	28,23	28,23	4 300	3,8 .10⁶
	5	29,87	29,87	25 00	21,9 . 10⁶
	10	29,96	29,96	48 00 (~ 5 cm)	40 . 10⁶
Proton	1	1,39		21,6
	5	3,1		350
	10	4,39		1 220
Particule a	1	0,69	0,69	6,8	6,9 . 10³
	5	1,55	1,55	33,2	34 . 10³
	10	2,19	2,19	103,3 (~ 0,1 mm)	102 . 10³ (~ 10 cm)

		Travailleurs	Apprentis et étudiants (de 16 à 18 ans)	Femmes enceintes (grossesse déclarée)
Dose efficace		20	6	Les dispositions prises pour l’exposition de la femme dans son emploi doivent être telles que l’exposition de l’enfant à naître soit aussi faible que raisonnablement possible et en tout état de cause en dessous de 1 mSv.
Dose équivalente	Cristallin	150	50
	Mains, avant–bras, pieds et chevilles	500	150
	Peau (dose moyenne sur 1 cm²)	500	150

		Valeur moyenne	Valeur élevée
Radiations cosmiques		0,4 mSv (au niveau de la mer)	2 mSv (en altitude)
Radiations du sol		0,5 mSv	40 mSv
Radiations lors de radiodiagnostic		1 mSv	20 mSv
Radiation naturelle		2,5 mSv
Expérience médicale (un seul examen)	Radio pulmonaire	0,3 mSv
	Radio abdominale	1 mSv
	Scanner thorax	5 mSv
	Scanner abdominal	2 à 15 mSv
	Traceur Scintigraphie osseuse	4 mSv
	Traceur Scintigraphie cardiaque	20 mSv
Traitement de doses absorbées localement pour détruire des tissus tumoraux (radiothérapie et curiethérapie)		10 000 à 100 000mGy
Opérateurs de centrale		2,5 mGy
Manipulateurs de radio en médecine		0,5 mGy
Pilotes d’avion (selon l’altitude)		2 à 3 mGy
Mineurs (confinement et minéraux)		1 à 10 (plus risque de grisou)

Énergie de l’électron T :	2 MeV	5 MeV	10 MeV
Parcours pour un arrêt total dans l’eau :	1 cm	2,5 cm	5 cm

Généralités

Tout est discontinu

A A 0

X " Y + b+ + 1 neutrino

Z Z–1 1

A A

X " Y + bˉ + 1 antineutrino

Z Z+1

Après cela devient vite impossible, même pour un ordinateur…

C’est déjà fini avant d’avoir commencé…

Même avec 2 forces seulement, c’est déjà compliqué…

Donc 1 u.m.a = = 1,66 . 10–27 kg

E = =

E = 30,85

Réglage Lecture Étalonnage

B avec une erreur DB

Nombre de fois

que l’on trouve

Or, avec la mécanique classique c’est impossible : remise en cause totale !

Impulsion d’une particule = p = m.v =

Interactions du rayonnement avec la matière

Y

A A–4 4 A–4

X " Y* + a " Y + g

Z Z–2 2 Z–4

Quelques exemples :

6 7

n + Li " Li

3 3

1 10 4 7

n + B " a + Li

0 5 2 3

113 114

n + Cd " Cd + g

158 159

n + Gd " Gd + g

Dosimétrie

Qu’est–ce que c’est que ces bêtes là ?

" Mais qu’est–ce que cette dose ?

Presque vrai… à un petit détail près…

Il n’est pas anodin de prendre l’activité en Curie : on enlève un 1010 !

Cs

Ba

C’est grave docteur ?

X

C* B

C

Compteur

On peut diriger notre plus grande admiration

Origine des rayonnements

Processus atomique

Personne ne comprend pourquoi…

Mais pour l’électron : quelle est l’énergie de référence ?

Alors pourquoi des longueurs d’ondes précises ?

Il fixe des moments cinétiques s = n.h avec s = m.v.r et h = h/2p h = 6,62 . 10–34 J.s–1

On entre dans la mécanique quantique…

Avec r0 = h 2 /(m. e2) . 4.π.e0 = 0,53 Å

Avec se = constante d’écran des autres électrons.

E l K = EX1 + EX2 + EX3 EX1 = E l MV ; EX2 = E l LIII – E l MV ; EX3 = E l K – E l LIII

Origine des rayonnements

Processus nucléaire

Noyau lourd " 2 noyaux légers

Qu’est–ce qui nous intéresse dans ce processus ?

Temps

Temps

Temps

N0

Temps

Temps

On remarque que NB part de 0 et va vers 0.

Hum hum…

Temps

NB(t) Temps

_{A A 0}

X " Y + b⁺ + 1 neutrino

_{A A}

Donc 1 u.m.a = = 1,66 . 10^–27 kg

_{A A–4
4 A–4}

^{Z Z–2
2 Z–4}

_{6 7}

^{3 3}

_{1
10 4 7}

^{0
5 2
3}

_{113 114}

_{158 159}

Il n’est pas anodin de prendre l’activité en Curie : on enlève un 10¹⁰ !

Il fixe des moments cinétiques s = n.h avec s = m.v.r et h = h/2p h = 6,62 . 10^–34 J.s^–1

Avec r₀ = h² /(m. e²) . 4.π.e₀ = 0,53 Å

Avec s_e = constante d’écran des autres électrons.

E _l_K = E_X1 + E_X2 + E_X3 E_X1 = E _l_M_V ; E_X2 = E _l_L_III – E _l_M_V ; E_X3 = E _l_K – E _l_L_III

N₀

On remarque que N_B part de 0 et va vers 0.

N_B(t) Temps